Torsion
Definition
Given a manifold with a covariant derivative operator $(M,\nabla)$, we can define a tensor named torsion as
$$ T (u, v)= \nabla_u v- \nabla_v u-[u,v] $$Or, in Penrose abstract index notation:
$$ T_{ab}^c X^a Y^b=X^m \nabla_m Y^c-Y^m \nabla_m X^c-[X,Y]^c $$Interpretation
Since we know that the Lie bracket $[u,v]$ measures the fail to close a rectangle along flow lines of $u$ and $v$, $T (u, v)$ measures the fail to close a rectangle made of parallel transported vectors along the flow, as you can observe in the picture (taken from here:
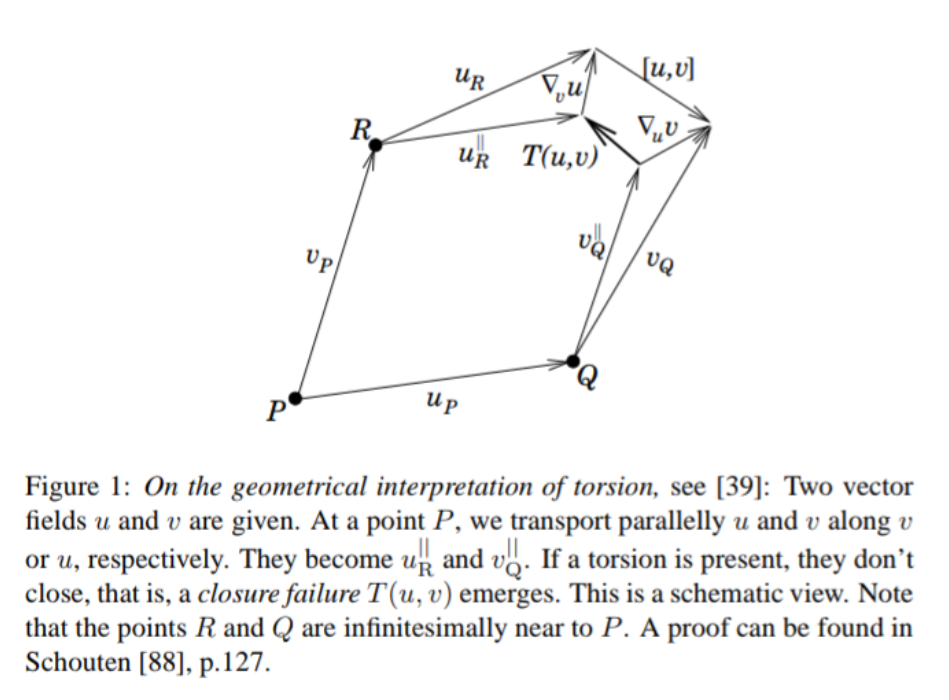
Personal thought: I think it should be defined independently of the Lie bracket, in a way that reflects more intrinsically the idea of "the fail to close a rectangle made of parallel transported vectors along the flow".
Explanation (see better relation of Lie derivative, covariant derivative and torsion): observe that, as it has been said here,
$$ \nabla_u v=\lim_{\epsilon \to 0} \dfrac{(v_Q)_{\parallel}(Q\to P)-v_P}{\epsilon} = $$ $$ =\lim_{\epsilon\to 0}\dfrac{v_Q-(v_P)_{\parallel}(P\to Q)}{\epsilon}\asymp \dfrac{v_Q-(v_P)_{\parallel}(P\to Q)}{\epsilon} $$and so
$$ \nabla_{\epsilon u} v\asymp v_Q-(v_P)_{\parallel}(P\to Q) $$In the (schematic) picture above, since $Q$ is considered infinitesimally near to $P$, this is translated as
$$ \nabla_u v =v_Q-v^{\|}_Q $$And analogously
$$ \nabla_v u =u_R-u^{\|}_R $$On the other hand, observe that according to this, we have
$$ [u,v] \asymp u_P+v_Q-(v_P+u_R) $$and therefore the quantity
$$ T (u, v)= \nabla_u v- \nabla_v u-[u,v]\asymp $$ $$ \asymp v_Q-v_Q^{\|}-(u_R-u^{\|}_R)-(u_P+v_Q-(v_P+u_R))= $$ $$ =v_P+u_R^{\|}-(u_P+v_Q^{\|}), $$which is the gap of the parallelogram made of parallel transported vectors (along infinitesimally short curves $PQ$ and $PR$!). This can be fully formalized working in a local chart and using Taylor expansion (see xournal_166).
Almost always, the given connection is torsion free (for example, the Levi-Civita connection). So it turns out that
$$ [u,v]=\nabla_u v- \nabla_v u $$Expression in coordinates
It can be shown that for any connection, in coordinates,
$$ T_{i j}^{k}=\Gamma_{i j}^{k}-\Gamma_{j i}^{k} $$i.e., the difference of the Christoffel symbols, in case it is the Levi-Civita connection.
Since it is a torsion free connection, Christoffel symbols are symmetric.
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: